[Algo] Insertion Sort - 삽입 정렬

참고한 블로그 : https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html

[알고리즘] 삽입 정렬(insertion sort)이란 - Heee's Development Blog

알고리즘을 풀다 내가 삽입 정렬도 구현하지 못하는 것을 발견했고, 잊지 않고자 기록한다...

먼저 삽입 정렬이란 다음과 같다. (오름차순 정렬이라고 가정)

https://ko.wikipedia.org/wiki/%EC%82%BD%EC%9E%85_%EC%A0%95%EB%A0%AC

삽입 정렬 - 위키백과, 우리 모두의 백과사전

삽입 정렬은 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다.

정렬되지 않은 배열의 요소중 가장 앞 요소를 정렬된 배열의 맨 뒤에 삽입, 자기보다 작은 요소가 나올 때까지 앞의 요소와 자리를 계속 바꾼다.
결국 정렬된 배열에 삽입 후 다시 정렬된 상태가 된다면, 정렬되지 않은 배열에서 수를 하나 다시 가져와 삽입한다.
이 과정을 반복하는 것이 삽입 정렬이다.

 

삽입 정렬을 시각화해서 나타내 보겠다.

10, 7, 1, 3, 2, 4를 가지는 정렬되지 않은 배열이다.

앞에서 '정렬된 배열'과 '정렬되지 않은 배열' 두 배열을 사용했었는데, 실제로는 배열 하나로도 구현이 가능하다. (부분을 나눠서 사용)

다음과 같이 배열의 맨 앞에 크기를 가지지 않는 '정렬된 배열' 이 있다고 생각해보자.

이 배열에는 아무것도 담기지 않았으므로 크기 = 0이고 요소가 없으므로 이미 정렬된 상태라고 해도 무방하다.

 

여기에 idx = 0인 요소를 하나 추가해보자. 

그럼 정렬된 배열에는 요소가 1개이므로 정렬된 상태가 유지되어 다음 요소를 삽입할 준비를 마친다.

 

앞의 빨간색 부분이 정렬된 배열이다.

이제 idx = 1인 요소를 삽입해 보겠다.

정렬된 배열에 7을 삽입해 정렬되지 않은 상태가 되었다.

이제 7은 자기 앞의 요소보다 클 때까지 앞으로 가기를 반복한다.

초록색 화살표가 가리키고 있는 요소와 자신을 비교했을 때, 자신보다 크므로 (자기 앞의 요소보다 작음) 두 수를 바꿔준다.

다음 루프에서는, 초록색 화살표가 가리키는 부분이 0보다 작아져 루프를 멈춘다.

이제 다음 수를 삽입할 차례다.

idx = 2를 삽입, 자기 앞의 수와 비교한다.

자기보다 크므로 마찬가지로 자리를 바꿔준다.

그리고 초록색 화살표가 가리키는 idx > 0이므로 한번 더 비교를 수행한다.

여전히 자신보다 크므로 자리를 바꾼다.

초록색화살표_idx < 0이므로 루프를 멈추고 다음 수를 삽입한다.

3을 삽입한 후, 비교를 수행한다.

10보다 작으므로 두 수를 바꿔준다.

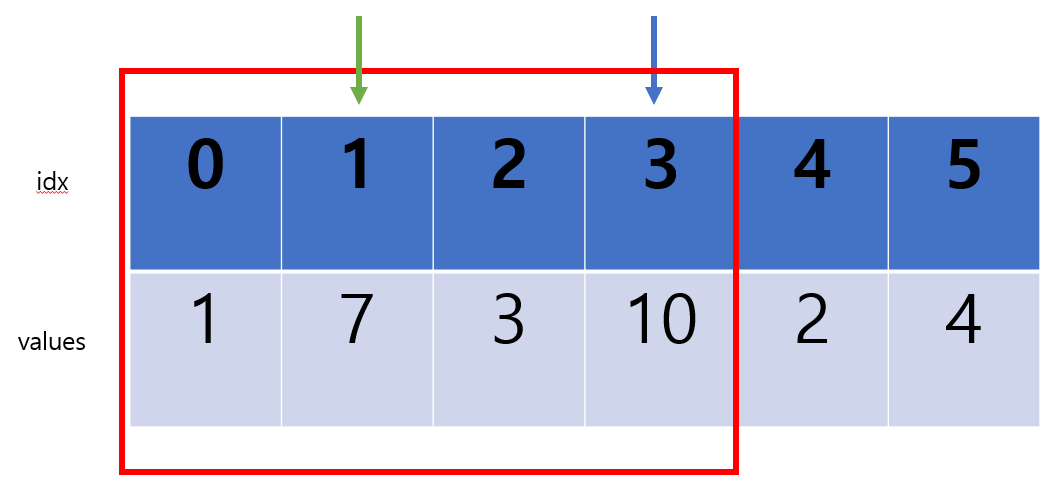
7 > 3이므로 역시 자리를 바꿔준다.

1 < 3 으로 자기 앞의 수보다 크므로, 반복을 멈추고 다음 수를 삽입한다.

마찬가지로 다음 숫자인 2를 삽입한다.

이번엔 한번 정렬 과정을 생각해보자. 2는 자기 앞의 수보다 클 때까지 계속 앞으로 가기를 수행하므로, 자기보다 작은 1을 만나기 전까지 계속 앞의 수와 swap을 진행할 것이다.

그렇다면 결국 순서는 1, 3, 7, 10, 2에서 1, 2, 3, 7, 10이 될 것이다.

그리고 1보다는 크므로 루프를 멈추고, 다음 수를 삽입한다.

역시 4도 자기 앞 수보다 작으므로, 계속 swap을 수행한다.

4는 자기보다 작은 3 뒤에서 멈추므로, swap이 멈추는 시점은 다음과 같을 것이다.

이제 다음 수를 삽입해야 하는데, 

파란색 화살표가 배열을 벗어나 더 이상 정렬을 진행할 필요가 없다.

정렬이 다 된 것이다.

이제 정렬이 끝났으니, 결과를 반환해주면 된다.

 

> 코드

설명을 들으면서 눈치가 빠른 사람들은 파란색 화살표가 i, 초록색 화살표가 j임을 깨달았을 것이다.

그럼 이제까지의 과정을 코드로 구현해보겠다.

// Test Source.
#include <iostream>
#define SIZE 6
using namespace std;
void swap(int*, int*);
int main() {
	int arr[SIZE] = { 10, 7, 1, 3, 2, 4 };
	int i, j;
	cout << "정렬되기 이전 배열 (arr) | ";
	for (i = 0; i < SIZE; i++)
		cout << arr[i] << " ";
	cout << endl;

	// insertion sort
	for (i = 1; i < SIZE; i++) {
		for (j = i - 1; j >= 0; j--) {
			if (arr[j] > arr[j + 1]) {
				swap(&arr[j], &arr[j + 1]);
			}
			else {
				break;
			}
		}
	}
	cout << "정렬된 배열 (arr) | ";
	for (i = 0; i < SIZE; i++)
		cout << arr[i] << " ";

	return 0;
}
// 두 수를 바꿔주는 swap 함수.
// 비트 XOR연산을 이용해 swap을 진행한다.
// 두 수가 같을 시에는 비트 연산을 하면 오류가 생겨 그냥 return
void swap(int* n, int* m) {
	if (*n == *m)
		return;
	*n ^= *m;
	*m ^= *n;
	*n ^= *m;
	return;
}