[Baekjoon] 9663_N-Queen #1
9663번: N-Queen
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다. N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.
N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)
출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.
먼저 이 문제를 해결하기 위해 필자는 이전 문제에서 배웠던 구조를 가져왔다.
함수 안에 반복문을 만들고, 그 반복문 안에 함수를 넣고 반환조건을 설정하여 백트래킹을 구현하는 구조이다.
하지만 그러려면 일단 Brute Force방법이 기초가 되어 시간이 아직 많이 걸리는 단점이 있다.
먼저 코드의 구조는 다음과 같다.
def n_queen(i, j):
global cnt
global board
global queens
for k in range(n**2):
if (i*n+j+k)//n >= n:
return # 보드 끝까지 갔을 때 -> 실패
if check((i*n+j+k)//n, (j+k)%n) == 1 and board[(i*n+j+k)//n][(j+k)%n] == 0:
board[(i*n+j+k)//n][(j+k)%n] = 2
queens += 1 # queen 추가
if queens == n: # 완성 되었을 때
cnt += 1
#print('complete')
#print_board()
queens -= 1
board[(i*n+j+k)//n][(j+k)%n] = 0
continue
next_j = (j+k)%n + 1
next_i = (i*n+j+k)//n
if next_j == n:
next_i += 1
next_j = 0
if next_i >= n: # 보드 끝까지 갔을 때 -> 실패
board[-1][-1] = 0
queens -= 1
return # end
n_queen(next_i, next_j)
queens -= 1
board[(i*n+j+k)//n][(j+k)%n] = 0
return
n_queen 함수는 좌표로 i, j를 입력받고, 거기서부터 뒤쪽으로만 가면서 queen을 놓을 수 있는 자리가 있다면 queen을 놓고, 다시 n_queen()을 호출한다.
n*n 이중 리스트인 board를 만들어 그 위에 queen을 2로 표시한다. 빈칸은 0으로 표시한다.
최대 n^2번을 탐색하므로 시간 복잡도는 n^2이다.
k번 반복할 때 행의 좌표와 열의 좌표를 계산하는 법은 나머지 연산과 몫 연산을 활용한다.
# 행
(i*n + j + k) // n
# 열
(j + k) % n먼저 행은 i 행 j 열이므로 n개 줄이 i 행이 있고, 거기에 j개의 열이 추가로 있으므로 총거리로만 따지면 반복 시 n*i + j + k개의 거리가 된다.
이때 행은 다시 n으로 몫연산을 이용해 나눠 준다(나머지는 열이 대신해주기 때문).
다음으로 열은 단순히 0부터 n-1까지의 수를 반복하므로 n을 나머지 연산해주면 구할 수 있다.
만약 호출시 queen의 개수가 n개 이상이라면, 완성되었단 뜻이므로 성공 사례를 세는 변수인 cnt를 1 추가하고 그 자리의 queen을 삭제, 반복문을 continue 한다.
그리고 만약 queen의 개수가 n이 되기 전 board의 끝에 도달한다면, 실패했다는 뜻이므로 board 끝에 놓인 queen을 제거하고 return 한다.
이때, queen을 놓을 수 있는 자리를 판단하는 함수는 check() 함수이다.
def check(y, x):
global board
k = 0
for i in range(n): # 가로, 세로
if board[i][x] != 0 or board[y][i] != 0:
return 0
# 오른쪽 아래로
if y - x >= 0:
for i in range(n - (y - x)):
if board[y-x + i][i] != 0:
if y != y-x+i and x != i:
return 0
else:
for i in range(n - (x-y)):
if board[i][x-y+i] != 0:
if y != i and x != x-y+i:
return 0
# 왼쪽 아래로
if x + y <= n - 1:
for i in range(x+y+1):
if board[i][x+y - i] != 0:
if y != i and x+y - i != x:
return 0
else:
for i in range(2*n - 1 - (x+y)):
if board[x+y- n + 1 + i][n - 1 - i] != 0:
if y != x+y- n + 1 + i and x != n - 1 - i:
return 0
return 1 # 가능만약 그 칸에 queen을 놓을 수 있다면 1을 return 하고, 아닐 시 0을 return 한다.
가로세로 대각선 2개를 반복하므로 최대 4*n개를 탐색한다. 따라서 시간 복잡도는 O(n)이다.
check함수를 최적화하기 전, 처음에는 Brute Force방식으로 모든 칸을 반복하며 그 칸의 가로, 세로, 대각선에 위치하면 다른 queen이 그 자리에 없는지를 찾았다. (O(n^2))
하지만 그렇게 하니 너무 시간이 많이 걸리는 문제가 생겼다.
그래서 필요한 칸만 검색하는 함수가 필요했고, 사용된 아이디어는 다음과 같다.
어떤 칸을 입력받으면, 그 칸에서 가로, 세로, 대각선에 다른 queen이 있으면 0을 return 하고 반복문이 끝날 때까지 나오지 않으면 1을 return 한다.
대각선이 구현이 좀 까다로웠는데, i와 j(현 좌표), n을 이용해 대각선으로 내려올 때 처음에는 "어디서 시작할지", "몇 번 반복할지"를 계산한다.
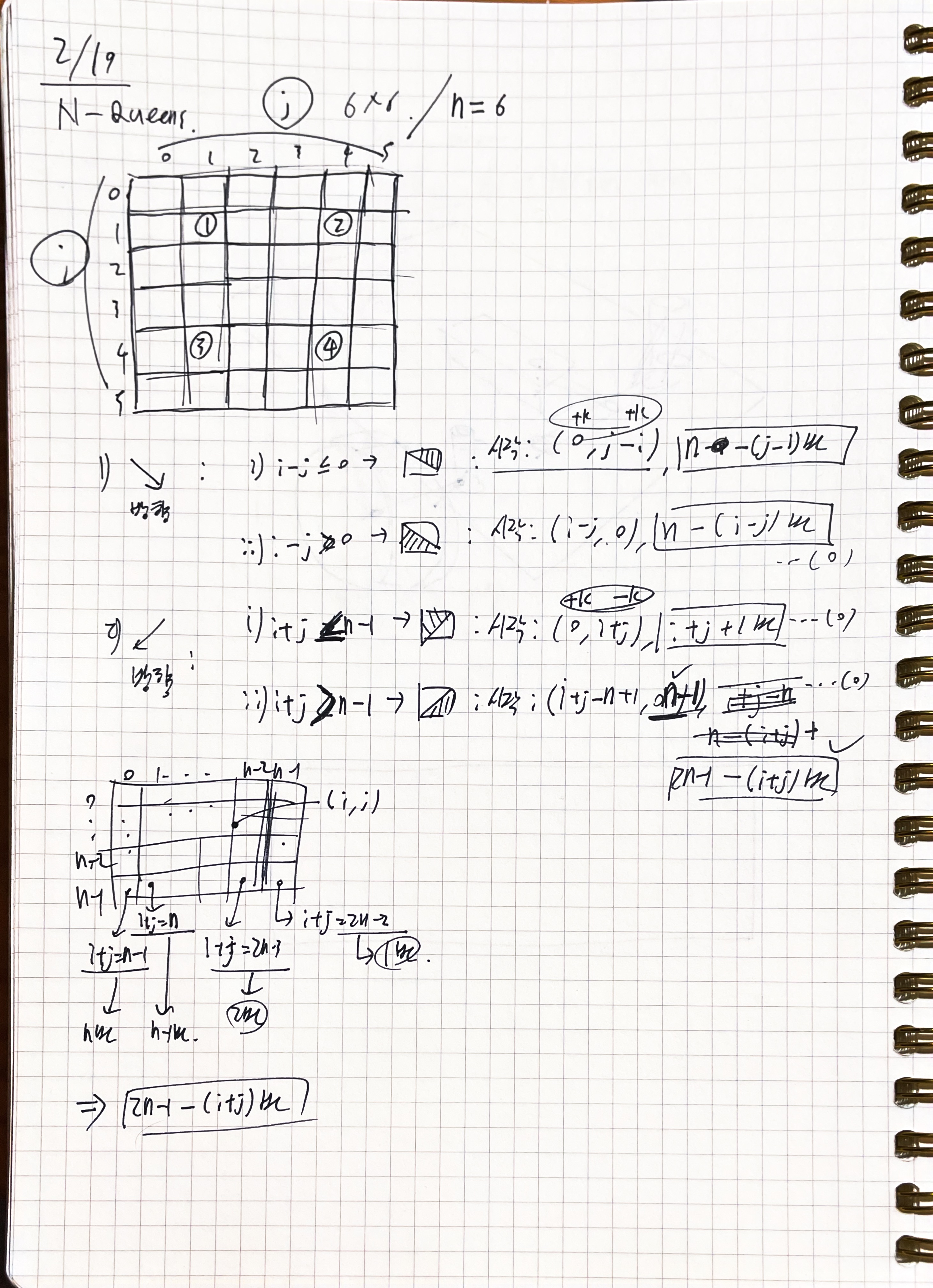
오른쪽 아래 방향: 각 대각선마다 i - j 가 고유한 값을 가지므로, 먼저 이를 0보다 작거나 크거나 같은 값으로 나누고, 각 케이스마다 어디서 시작해야 할지, 몇 번 반복해야 할지를 계산한다.
왼쪽 아래 방향 : 각 대각선마다 i + j 가 고유한 값을 가지므로, 마찬가지로 이번엔 n-1을 기준으로 케이스를 분류한다.
최적화 전후 걸린 시간을 비교하면 다음과 같다.


하지만 여전히 문제의 제한 시간은 10초이므로 다른 방법이 필요했다.
queen을 놓을 때 안 되는 자리를 표시하면 되지 않을까 하는 생각이 들 수도 있다.
하지만 그러면 그 queen을 지울 때 놓으면 안 되는 자리가 겹친다면, 다른 queen의 영향이 무시될 수 있다는 문제가 생긴다(어느 queen 때문에 이 자리가 안 되는지 모르므로)
그러다 아이디어가 떠올랐는데,
그 자리의 숫자를 +1씩 하는 것이다.
이러면 기존의 queen의 영향도 유지되고, 겹쳐도 문제없이 진행할 수 있다.
(다만 queen의 숫자를 -1로 바꿔줘야 하지만 아무래도 상관없다)
그래서 두 함수를 추가했다.
mark() 함수와 unmark() 함수인데,
mark함수는 queen이 놓아지면 그 queen의 영향력이 미치는 자리에 숫자를 +1씩 해주는 함수이고,
unmark함수는 반대로 queen이 지워질 때 그 queen의 영향력을 삭제해주는 (-1) 함수이다.
check함수와 기능은 비슷했기에 두 함수를 작성하기는 쉬웠다.
def mark(i, j):
for k in range(n):
if k != i and board[k][j] >= 0:
board[k][j] += 1
if k != j and board[i][k] >= 0:
board[i][k] += 1
# 오른쪽 아래로
if i - j >= 0:
for k in range(n - (i - j)):
if board[i-j + k][k] >= 0 and k != j:
board[i-j + k][k] += 1
else:
for k in range(n - (j-i)):
if board[k][j-i+k] >= 0 and k != i:
board[k][j-i+k] += 1
# 왼쪽 아래로
if j + i <= n - 1:
for k in range(j+i+1):
if board[k][j+i - k] >= 0 and k != i:
board[k][j+i - k] += 1
else:
for k in range(2*n - 1 - (j+i)):
if board[j+i- n + 1 + k][n - 1 - k] >= 0 and n - 1 - k != j:
board[j+i- n + 1 + k][n - 1 - k] += 1
return
def unmark(i, j):
for k in range(n):
if k != i and board[k][j] >= 0:
board[k][j] -= 1
if k != j and board[i][k] >= 0:
board[i][k] -= 1
# 오른쪽 아래로
if i - j >= 0:
for k in range(n - (i - j)):
if board[i-j + k][k] >= 0 and k != j:
board[i-j + k][k] -= 1
else:
for k in range(n - (j-i)):
if board[k][j-i+k] >= 0 and k != i:
board[k][j-i+k] -= 1
# 왼쪽 아래로
if j + i <= n - 1:
for k in range(j+i+1):
if board[k][j+i - k] >= 0 and k != i:
board[k][j+i - k] -= 1
else:
for k in range(2*n - 1 - (j+i)):
if board[j+i- n + 1 + k][n - 1 - k] >= 0 and n - 1 - k != j:
board[j+i- n + 1 + k][n - 1 - k] -= 1
return그리고 n_queen 함수에는 처음에 들어갈 때 check함수 부분을 단지 board의 그 자리를 0인지 체크하는 방식으로 바꾸었고, 대신 queen을 추가할 때나 삭제할 때 mark, unmark함수를 사용하도록 바꾸었다.
def n_queen(i, j):
global cnt
global board
global queens
for k in range(n**2):
if (i*n+j+k)//n >= n:
return # 보드 끝까지 갔을 때 -> 실패
#if check((i*n+j+k)//n, (j+k)%n) == 1 and board[(i*n+j+k)//n][(j+k)%n] == 0:
if board[(i*n+j+k)//n][(j+k)%n] == 0:
board[(i*n+j+k)//n][(j+k)%n] = -1
queens += 1 # queen 추가
mark((i*n+j+k)//n, (j+k)%n)
if queens == n: # 완성 되었을 때
cnt += 1
#print('complete')
#print_board()
queens -= 1
board[(i*n+j+k)//n][(j+k)%n] = 0
unmark((i*n+j+k)//n, (j+k)%n)
continue
next_j = (j+k)%n + 1
next_i = (i*n+j+k)//n
if next_j == n:
next_i += 1
next_j = 0
if next_i >= n: # 보드 끝까지 갔을 때 -> 실패
queens -= 1
board[-1][-1] = 0
unmark((i*n+j+k)//n, (j+k)%n)
return # end
n_queen(next_i, next_j)
queens -= 1
board[(i*n+j+k)//n][(j+k)%n] = 0
unmark((i*n+j+k)//n, (j+k)%n)
return그러자 다음과 같은 결과가 나왔다.

오히려 속도가 떨어지는 모습을 보여 줬는데, 필자의 생각으로는 mark, unmark함수가 check함수와 시간 복잡도 및 구조도 비슷할뿐더러 호출되는 횟수가 더 많아져 이렇게 된 것으로 추정된다.
아이디어가 떠오른다면 다음 글에서 소개하겠다.