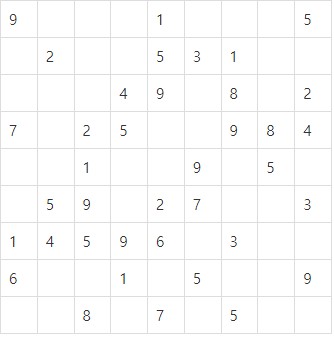
저번 글에 이어 이 글에서는 어려운 스도쿠를 풀 수 있는 프로그램을 설명한다.
백트래킹을 이용해 이를 구현했고, 생각보다 정말 간단하게 구현이 되었다.
먼저 사용된 함수는 다음과 같다.
def possibilities(i, j):
global sudoku
exist = []
for k in range(9):
if sudoku[k][j] != 0:
exist.append(sudoku[k][j])
if sudoku[i][k] != 0:
exist.append(sudoku[i][k])
if sudoku[i//3*3 + k//3][j//3*3 + k%3] != 0:
exist.append(sudoku[i//3*3 + k//3][j//3*3 + k%3])
unexist = [i for i in range(1, 10) if i not in exist]
return unexist # 리스트로 반환, 길이 0이면 가능한 수 없음possibilities() 함수는 위치를 인자로 받아 그 자리에 들어갈 수 있는 수를 리스트로 반환한다.
만약 가능한 수가 없다면 빈 리스트를 반환한다.
for 문 안에 들어 있는 if문들은 각각 열, 행, 칸을 검사한다.
정해진 개수의 칸만을 보기 때문에 시간 복잡도는 O(1)이다.

이때, 칸을 검사하기 위해 사용된 수식은 다음과 같다.
어느 칸에 있던지 좌표에 //3 * 3을 하면 그 칸의 왼쪽 상단으로 이동한다.(나머지 버림)
이를 이용해 칸을 검사했다.
def dfs(i, j):
global complete
global sudoku
if sudoku[i][j] == 0:
pos = possibilities(i, j)
for k in pos:
if complete:
return
sudoku[i][j] = k
#print(i, j, k)
next_i = i
next_j = j
while sudoku[next_i][next_j] != 0:
next_j += 1
if next_j == 9:
next_i += 1
next_j = 0
if next_i == 9:
for _ in range(9):
print(sudoku[_])
complete = 1
return # 완성
dfs(next_i, next_j)
sudoku[i][j] = 0
return
next_i = i
next_j = j
while sudoku[next_i][next_j] != 0:
next_j += 1
if next_j == 9:
next_i += 1
next_j = 0
if next_i == 9:
for _ in range(9):
print(sudoku[_])
complete = 1
return # 완성
dfs(next_i, next_j)
return본 프로젝트의 메인인 dfs함수이다.
어떤 칸을 입력받으면, 그 칸이 비어 있다면 가능한 수를 받고(possibilities() 이용) 다음에 비어 있는 칸으로 이동한다.(dfs() 이용)
'가능한 수'만을 시도하기 때문에 만약 이제까지의 칸들이 다 채워진 상태로 마지막 칸에 도착하면 complete를 1로 바꾸고 함수를 return 한다.
만약 끝까지 갔는데도 가능한 경우가 없다면, 스도쿠는 출력되지 않는다.
대략적인 알고리즘은 다음과 같다.

총 실행시간은 다음과 같다
case 1)

0.007초
hard1)
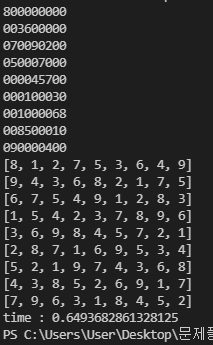
0.6초
이상으로 Python 스도쿠 풀이 프로그램 글을 마치도록 하겠다.
전체 코드는 여기 있다.
https://github.com/siejwkaodj/Sudoku
GitHub - siejwkaodj/Sudoku: 스도쿠 풀이 알고리즘
스도쿠 풀이 알고리즘. Contribute to siejwkaodj/Sudoku development by creating an account on GitHub.
github.com
p.s.
생각보다 실행시간이 너무 빨라서 놀랬다.
이럴 거면 n-queen도 빨리 좀 해주지....
그리고 이 코드를 이용해 백준 2580 스도쿠를 풀어 봤는데 풀렸다.
https://www.acmicpc.net/problem/2580
2580번: 스도쿠
스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루
www.acmicpc.net

은근히 최적화가 잘 되어 있는 듯 하다.
'개인 프로젝트' 카테고리의 다른 글
| [WEB] 스도쿠 풀이 프로그램 #4 (2) | 2023.12.07 |
|---|---|
| [개인 프로젝트] Python으로 2048 게임 만들기 #2 (0) | 2022.02.28 |
| [Python] 스도쿠 풀이 프로그램 #2 (0) | 2022.01.13 |
| [개인 프로젝트] Python으로 2048게임 만들기 # 1 (0) | 2021.12.15 |
| [Python] 스도쿠 풀이 프로그램 #1 (0) | 2021.12.10 |
![[Python] 스도쿠 풀이 프로그램 #3](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F7zbNp%2FbtrtO8B9e53%2FBkDSZsDY2oZWmZhhIeQNd1%2Fimg.jpg)