[Algo] 다익스트라 (dijkstra) 알고리즘

1. 서론

다익스트라 알고리즘이란, 그래프 상에서 한 정점에서 다른 (모든) 정점으로의 최단경로를 구하기 위해 사용되는 알고리즘이다.

인접 리스트와 우선순위 큐를 이용해 손쉽게 구현할 수 있다는 장점이 있어 많은 사람들이 사용한다.

2. 설명

먼저, 다음과 같은 그래프가 있다고 가정하자.

다익스트라 알고리즘은 먼저 시작점 자신의 거리를 0으로 두고 다른 갈 수 있는 모든 점들의 최단거리값 (dist[])를 업데이트한다.

업데이트시 만약 [현재 노드의 cost + 현재 가리키는 노드로 가는 edge의 cost] 값이 가리키는 노드의 dist값보다 작다면, dist를 업데이트한다.

 

그 다음, 방문하지 않은 다른 모든 점들중 가장 dist값이 작은 노드를 시작점으로 잡고, 다시 dist를 업데이트한다.

 

이를 방문하지 않은 점이 없을 때까지 반복한다.

 

 

실제로 예시를 들어 설명해보겠다.

먼저 최단거리를 저장하는 dist 배열을 하나 만들고, INF값 (보통 10^9나 2^31 - 1로 초기화한다.)으로 초기화한다.

a를 시작점으로 잡고, 다익스트라 알고리즘을 사용하면, 먼저 a와 연결된 b, c, e의 cost가 각각 30, 10, 100으로 업데이트된다.

그럼 dist 배열은 다음과 같이 된다.

그런 다음, 방문하지 않은 점 중 가장 dist값이 작은 점 하나를 선택한다.

여기서는 a를 방문했으므로, b~e중 가장 dist값이 작은 점은 c이므로 c에서 다시 경로값을 계산하기 시작한다.

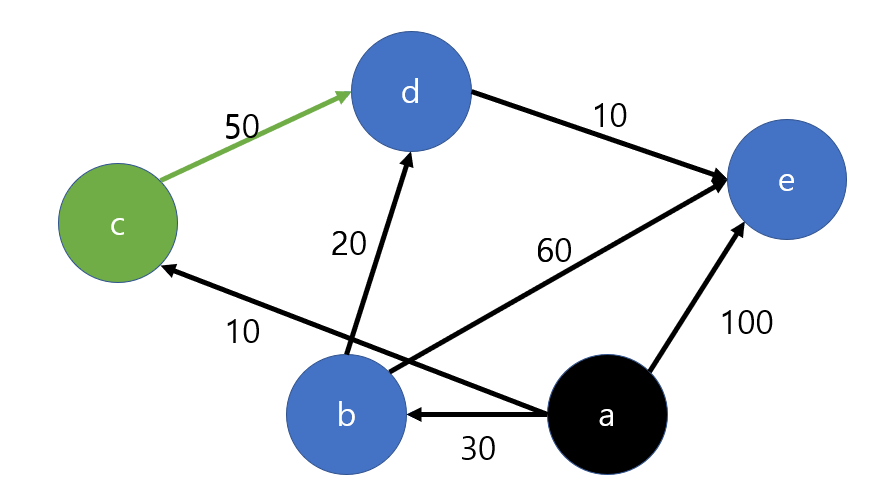
c에서 cost를 업데이트해주면, 연결된 간선이 c-d밖에 없으므로 d의 dist가 다음과 같이 업데이트된다.

이때, d의 dist값은 dist[c](10) + edge[c][d](50) = 60 < INF 이므로 60으로 업데이트된다.

 

그 다음 방문하지 않은 노드 중 가장 cost가 작은 노드는 b이므로 b에서 탐색을 계속한다.

b에서 d와 e의 dist값을 각각 비교하면, 

dist[d](60) > dist[b](30) + edge[b][d](20) 이므로 dist[d]값을 50으로 업데이트한다.

dist[e](100) > dist[b](30) + edge[b][e](60) 이므로 dist[e]값을 90으로 업데이트한다.

 

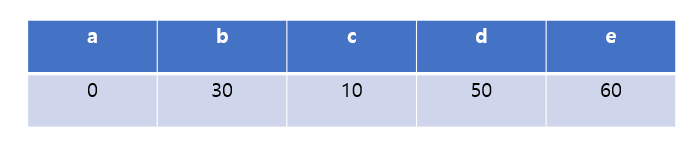
최종 dist값은 다음과 같다.

 

그리고 남은 노드 중 최소 dist값을 가진 노드는 d이므로 d에서 탐색을 계속한다.

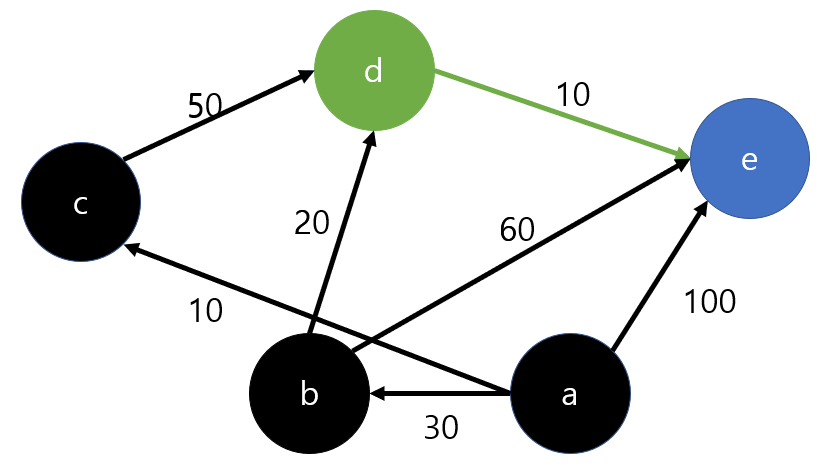
d에서 탐색을 계속하면,

dist[e](90) > dist[d](50) + edge[d][e](10) 이므로 dist[e]값을 60으로 업데이트한다.

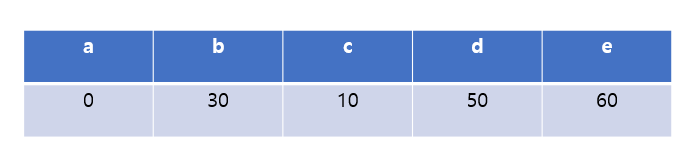
그리고, 그 다음 최소 비용을 가진 노드인 e로 가서 탐색을 계속하면,

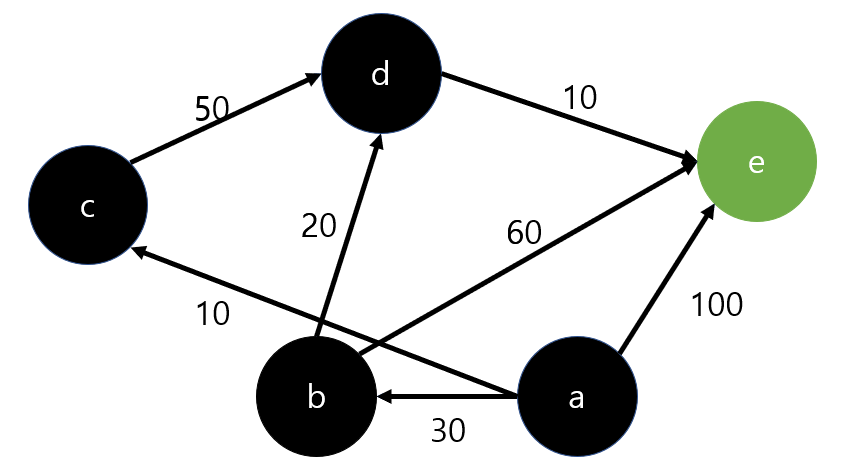
e에서는 더 이상 방문할 수 있는 노드가 없기 때문에 넘어가고, 더 이상 방문할 수 있는 노드가 없기 때문에 알고리즘을 종료한다.

 

최종적으로 a에서 다은 모든 노드로 갈 수 있는 최단 경로는 dist[] 배열이 된다.

3. 실습 코드

c++로 짠 코드는 다음과 같이 된다.