유전 알고리즘으로 사이클로이드 유도하기 [1]

Making Cycloid by Genetic Algorithm

0. 개요

사이클로이드가 최소 강하 곡선인 이유를 탐구하다, 해당 내용을 보고 사이클로이드를 유도하는 방법을 알게 되었다.
https://suhak.tistory.com/88

사이클로이드(cycloid)

또한 여기서 사이클로이드를 그릴 수 있었는데, 해당 코드는 다음과 같다.

from math import sin, cos, pi import numpy as np import matplotlib.pyplot as plt def cycloid(r): x = [] #x좌표 리스트 만듦 y = [] #y좌표 리스트 만듦 for theta in np.linspace(0, np.pi, 10): #theta변수를 -2π 에서 2π 까지 반복함 x.append(r*(theta - sin(theta))) #x 리스트에 매개변수함수값을 추가시킴 y.append(10 -(r*(1 - cos(theta)))) #y 리스트에 매개변수함수값을 추가시킴 plt.figure(figsize=(pi*2, 4)) # 그래프 비율 조정 plt.plot(x,y) #matplotlib.piplot을 이용해 그래프 그리기 plt.title('Cycloid') plt.xlabel('x') plt.ylabel('y') plt.xlim([0, 5*pi]) plt.ylim([0, 10]) plt.show() #그래프 출력하기 cycloid(5)

다음 코드를 실행시키면 밑의 사진과 같은 결과가 나온다.

하지만, 뭔가 부족함을 느끼고 뭔가 더 프로젝트를 진행할만한 게 없을까 하고 생각하던 중 유튜브 알고리즘에서 본 유전 알고리즘이 떠올라



이와 관련하여 다음과 같은 생각을 하게 되었다.

유전 알고리즘으로 최속 강하 곡선을 유도해보면 어떨까?

그리고 구간별로 직선의 기울기를 유전자로 설정할 수 있겠다는 아이디어가 떠올라 최종적으로 해당 실험을 설계하게 되었다.

++필자가 본 유튜브 영상은 다음과 같다.

 

https://youtu.be/Yr_nRnqeDp0?si=521tPT9G1VCtlWkl

https://youtu.be/WZnf0C8HfJc?si=Xeub6hk_5ercAtTw

 

 

1. 실험 설계

유전 알고리즘을 만들기 위한 조건은 간단하다.
우리가 구하고 싶은 해를 염색체의 모양으로 표현할 수 있어야 한다.

위의 그래프를 구간별로 자른 다음, 구간별로 기울기가 일정한 직선을 놓고, 그 기울기의 배열을 알고리즘의 해로 설정하면 유전 알고리즘을 적용할 수 있다.

< 처음 실험을 설계할 때 그래프 / 화질이 안 좋은 것은 그냥 넘어가자... >

또한, 등가속도 운동 공식을 이용, 구간의 길이와 처음 속도, 구간 가속도를 이용해 나중 속도와 걸린 시간을 구할 수 있다.

< 실험 설계 과정 >

(나중에 알게 된 사실인데, 에너지 보존을 이용하여 나중 속도를 구하면 구간의 길이를 따로 구하지 않아도 걸린 시간을 구할 수 있다.)

< E보존을 이용하여 나중 속도를 구하는 방법 >

따라서 걸린 시간은 다음과 같다.

우리는 기울기를 알고 있으므로, 직각삼각형 또는 삼각함수를 사용해 빗면의 가속도를 구할 수 있다.

< 기울기 구하는 과정,  >

• ## 주의
• 이때 기울기가 양수여야 나중 속도를 증가시킬 수 있으므로 해당 기울기에 절댓값을 해줘야 한다.

이때, 걸리는 시간을 정리해서 나타내면 다음과 같다.

< 근호 안의 수는 양수여야 하므로, 절댓값을 씌워 주는게 맞다>

코드상에서는 구간별로 걸리는 시간을 먼저 구한 다음, 시간을 비용이라 생각하여 적합도를 판단한다.

유전 알고리즘에서 가장 핵심적인 요소인 적합도를 어떻게 표현할지 고민하다, 사이클로이드 공식을 이용해 구한 최소 시간을 현재 도출된 시간으로 나누고, 이를 제곱하였다.(적합도 차이가 두드러지도록)

def fitness(t): #arr : sum_time입력받음 #별로 차이가 나지 않아 제곱을 해 주는 것이 좋을 것 같음 f = (T/t)**2 * 100 return f

실험을 구상할 때 가장 고민했던 것이 돌연변이를 일으키면 기울기의 합이 달라지는데, 기울기합 × 구간 길이 = 총 구간의 높이인데 이게 달라지면 바닥을 뚫고 내려가거나, 끝까지 내려오지 않을 수 있다.

구간을 정하고, 이 구간을 따라 내려가는 곡선을 구하는데, 이때 가다가 구간을 넘어버리면 아무 소용이 없지 않은가...

그래서 이 기울기 합을 일정하게 맞춰주기 위해 몇 가지 방법을 생각해봤다.

1. 기울기의 합을 구하고, 이를 구간의 높이와 비교한 다음, 차이나는 만큼의 비율의 역수를 각각 기울기에 곱해주는 것.
2. 마찬가지로 기울기 합을 구한 다음, 차이를 구하고, 이 차이를 구간의 개수만큼 나눠 각각 기울기에 빼주는 것.
3. 곡선이 바닥을 뚫고 내려가면 그 뚫고 내려간 다음 지점부터 직선 운동하도록 만드는 것.
4. 짝수/홀수 번째 기울기만 이를 변경시켜주는 값으로 삼는 것
5. 양 끝 값만 이를 보완해 주는 값으로 삼는 것

여기서 3. 은 구현이 어려워 일단 미뤄 놨고, 4. 5. 는 각각의 기울기가 변화하는 값이 너무 클 것 같아 제외했다.
1. 과 2. 를 고민하던 중, 결국은 결과가 같다는 것을 깨닫고, 구현이 간단한 1.로 채택했다.

  앞으로 이를 정규화(Generalization)로 부르자.  

곡선을 정규화를 시켜 주면, 총구간의 높이에 맞춰 곡선을 조정해준다. 따라서 곡선이 설정한 범위를 이탈할 걱정은 하지 않아도 된다.

하지만, 역시 문제는 남아 있는데, 하나의 기울기에서 돌연변이가 발생해도, 전체 값들에 영향을 준다는 것이다.
필자는 아직 해당 문제를 완벽히 해결하지 못했고, 아마 3. 또는 5. 가 더 좋은 최적해를 구하는데 도움을 줄 수 있을지도 모르겠다.
(좋은 방법이 있다면 댓글로 알려주세요)

또한, 기울기가 양수 범위에서 설정될 수 있다면, 기울기가 너무 커져 못 올라가는 경우가 생길 수 있으므로, 음수 또는 0의 값만 가질 수 있도록 했다.

2. 실험 진행

실험을 진행하기에 앞서, 먼저 0세대를 만든다.
0세대는 완전 무작위로 생성되며, 매 세대마다 우수한 10% 유전자를 다음 세대로 유전시킨다.

< 반영 비율 >

이전 세대에서 유전된 10%의 유전자를 이용해 위 비율대로 교차, 돌연변이를 일으켜 다음 세대로 유전시킨다.
돌연변이가 일어날 확률과 돌연변이 시 바뀔 수 있는 최대 비율을 설정하고, 이를 통해 돌연변이를 일으킨다.
돌연변이를 일으키는 이유는, 지역 최적해에 갇히는 것을 방지하기 위함이다.

또한 유전적 다양성을 위해 10%는 무작위 생성으로 만들었다.

교차 시에는 2점 교차라는 방법을 사용하였다.(밑의 링크 참고)
https://blog.devkcr.org/entry/%EC%9C%A0%EC%A0%84-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B0%80%EC%A7%80%EA%B3%A0-%EB%86%80%EA%B8%B0

유전 알고리즘 가지고 놀기

3. 결과

사이클로이드 그래프

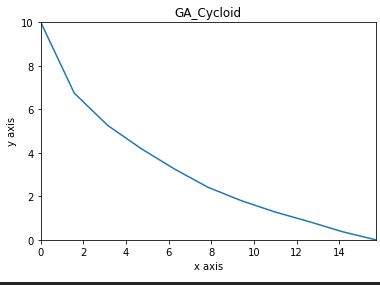
유전 알고리즘을 통해 생성된 그래프(적합도 = 93.00749419331%)

둘이 꽤 비슷한 모습인 것을 알 수 있다.

또한, 세대별 최대 적합도, 평균 적합도, 최저 적합도 그래프를 그려 보았다.

max_gen = 10000
min_m = -10
mut_chance = 0.2
mut_rate = 0.2일 때의 그래프이다.

최종 결과는 다음과 같았다.

gen : 1368
max fitness : 93.00250925477336
여기서 gen은 해당 그래프가 도출된 세대를 의미한다.
1368이면 비교적 처음 부분에 속한다.
즉 상위 10% 유전자를 유전시키던 도중, 지역 최적해(local minimum)에 갇힌 상황이라고 볼 수 있다.


따라서, 최종 적합도를 올리기 위해 돌연변이율을 바꿔 가며 그래프를 그려 보았다.

max_gen = 20000
min_m = -10
mut_chance = 0.6
mut_rate = 0.5로 설정했을 때이다.

gen : 639 max fitness : 92.6552349926282
그리 효과가 없는 듯하다.

여기서 mut_chance와 mut_rate, 즉 돌연변이가 일어날 확률이나 돌연변이율을 올린다면 평균 적합도가 요동치는 것을 알 수 있다.
유전적 다양성이 높아지는 것이다.
평균 적합도가 이렇게 요동치는 대에는 무작위 10%의 힘이 큰 것 같다.
하지만 최종 적합도를 올리는 데에는 별로 기여를 하지는 못했다.(상위 10%만 선택)
룰렛 휠 방식을 사용해 무작위 유전자와 교차시키는 방법을 고려해 봐야겠다.

mut_rate를 0.2, mut_rate = 0.4로 해 보았다.

gen : 4173
max fitness : 92.75082693395207

mut_chance = 0.6
mut_rate = 0.2로 설정했을 때이다.
마찬가지로 처음보다는 평균 및 최저 적합도가 요동친다.

gen : 8838
max fitness : 92.7141370571032
그러나, 모두 최대 적합도 94%를 넘기지 못했다. 93. 대에서 머무르고 있다.
그리고, 두 번째 경우에 비해 최고 적합도가 후반부에서 나온 것으로 보아, 최적해에 다가가는 속도가 느린 것 같다.

아마 유전자를 교차시키는 방법을 수정하는 것에서 해결책이 나올 것 같다.

4. 느낀 점

영상으로 볼 때는 쉬워 보였는데, 막상 해보니까 아니었다.
시간은 총 4일 정도 소요되었고, 그리 만족할만한 결과도 도출되지 못했다.

이번 프로젝트를 진행하며 얻은 점은,

1. 최적화 프로그램에서는 지역 최적해에 갇히는 것을 해결하는 것이 중요하다. 이를 해결하는 다양한 방법이 현재 AI의 최적화 함수에 사용된다. 대표적인 최적화 함수로는 바로 그 Adam이 있다.

2. python을 이용하여 그래프를 그리는 matplot.lib을 사용하는 법을 알게 되었다. 실제로 공을 떨어뜨려 내려오는 것을 보여주는 프로그램을 이용할 수 있었다면 좋았겠지만, 아쉽게도 찾지 못해 그냥 그래프로 만족했다.

3. 자녀 수와 세대를 줄여도 첫 세대에서 적합도 90%를 넘기는 자손은 거의 무조건 한 마리 이상 나온다. 이를 통해 어느 집단이나 1등은 뛰어나다는 것을 알게 되었다.

4. 자손의 '분포'가 일정한지 아닌지도 영향을 미친다는 것을 알게 되었다.

#무작위 생성 for j in range(x_size): theta = rand(atan(min_m), 0) #-2 이상 0 미만 실수값 입력, 단위 라디안 #10개 숫자 평균적 합이 10이 되도록 맞춰줌 randM = tan(theta) #randM = rand(-2, 0) # 기울기 자체를 랜덤값으로 결정

코드에서는 무작위로 자손을 생성할 때, θ값을 무작위로 생성하고, 이를 기울기로 변환하는 방법을 사용한다.
기울기를 바로 생성하는 방법도 있지만, θ를 무작위로 분포시키는 것과 기울기를 분포시키는 방법을 사용하는 것이 적합도 분포에서 다른 결과를 가져올 수도 있다는 점에서 착안하였다. (실제로는 영향이 그렇게 크지 않다.... 0세대에서 10%만 걸러내서 그런 것 같다.)

여러 번 사건을 시행하면 그 확률은 대수적 확률에 수렴한다는 '대수의 법칙'에 기반하여 해당 프로젝트는 설계되었기 때문에, 이 분포에도 신경을 썼다. (더 나은 방법이 있다면 댓글로 알려주세요)

5. 직접 프로젝트를 설계하고 진행하며 멘탈관리도 중요하다는 점을 알게 되었다. 그리고 중간중간 느낀 점이 있다면 바로바로 문서화를 하는 것이 더 편하다는 것을 알게 되었다. 또한 다른 선행 연구를 참고하며 프로젝트를 진행하였는데, 역시나 선행 연구의 중요성을 알게 되었다.


해당 알고리즘의 코드는 아직 수정중이지만, 나처럼 프로젝트를 진행하는 이들을 위해 일단 올려둔다.
https://github.com/siejwkaodj/Making-Cycloid-by-Genetic-Algorithm/blob/main/GA_Cycloid.py

GitHub - siejwkaodj/Making-Cycloid-by-Genetic-Algorithm: Making Cycloid by Genetic Algorithm

p.s. 인용시 댓글 한번씩만 달아주세요~