유전 알고리즘으로 사이클로이드 유도하기 [2]

지난 포스팅에서는 유전 알고리즘을 통해 사이클로이드를 유도하는 법을 알아보았다.
하지만 교차 및 돌연변이 방식, 기울기를 정하는 방식, 정규화 방법 등 아직 개선점이 많이 필요한 모습을 보였다.

그중 무엇보다 적합도가 93% 이상 올라가지 않던 문제가 가장 해결하기 어려웠다.

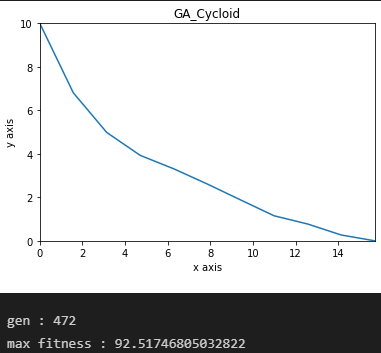
max_gen = 1000
num = 100
min_m = -10
mut_chance = 0.3
mut_rate = 0.4로 돌린 결과이다.

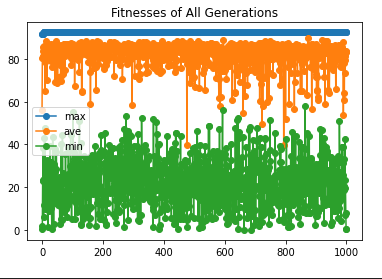
사진과 같이 최고 적합도는 크게 올라가지 않는 모습을 보여준다.
여기서 필자는 교차 및 돌연변이 방법에 문제가 있다고 생각해 해당 방법을 고민하던 중,
해당 프로그램을 보던 한 친구가 구간의 길이를 줄여보자는 아이디어를 건의했다.
현재 유전 알고리즘은 가로 5π, 세로 10인 공간 속에서 돌아간다.

< 사이클로이드 곡선 >

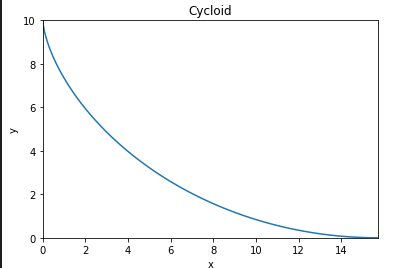
필자는 가로 구간을 10개로 나눠 사이클로이드를 유도하려 하였다.
그런데 실제 사이클로이드는 곡선이다.
직선을 이어 아무리 최단 강하 곡선을 만들어도 그 한계가 있는 것이다.
그래서 구간의 크기를 줄여 구간의 수를 늘리면 훨씬 적합도가 올라갈 여지가 있는 것이다.

< 구간을 20개로 쪼개 보았다 >

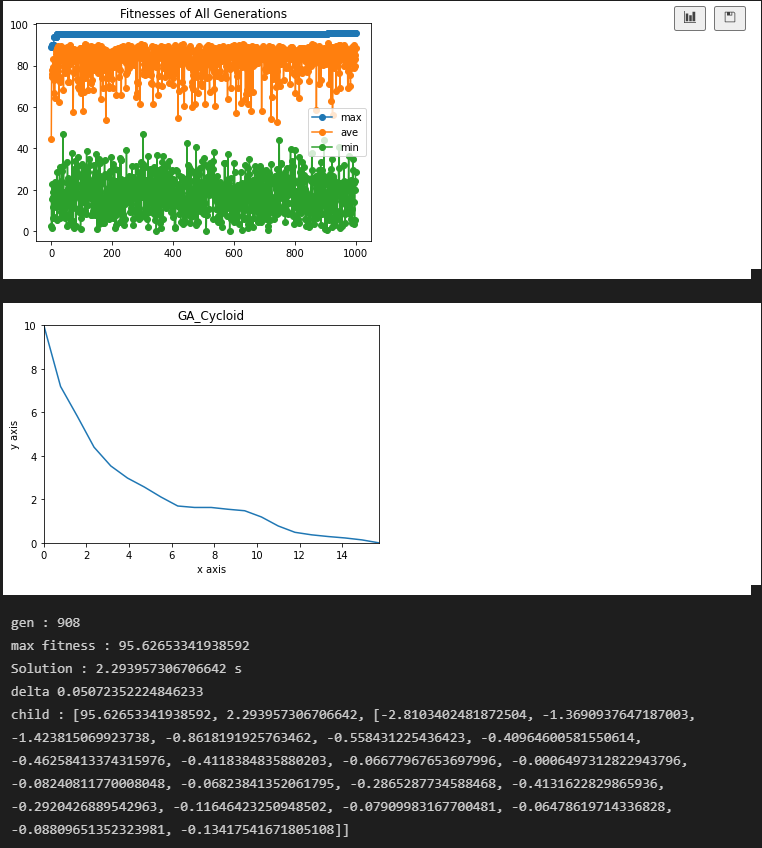
구간을 20으로 늘리고,
조건은 위와 똑같이 설정하였다.

max_gen = 1000
num = 100
min_m = -10
mut_chance = 0.3
mut_rate = 0.4

... 깨지지 않던 93%의 벽이 무너졌다.

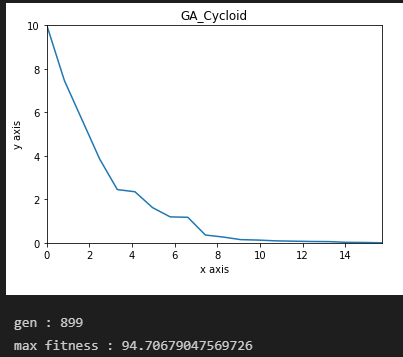
게다가, 그래프의 모양을 보면 아직 개선의 여지가 있는 듯하다.

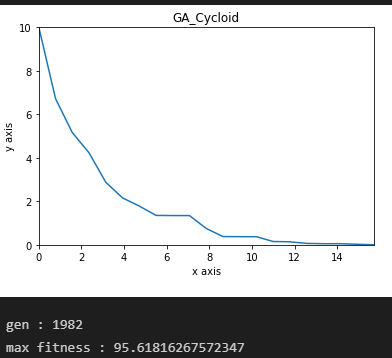
혹시나 해서 max_gen을 5000으로 해서 돌려 봤지만, 아직까지는 초반의 우수한 유전자 몇 개의 영향을 크게 받는 것 같다.

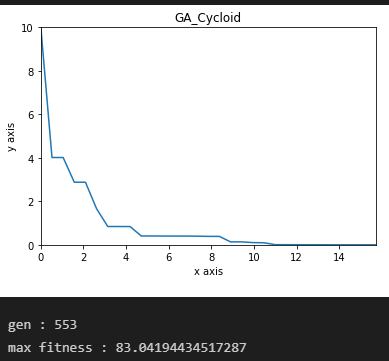
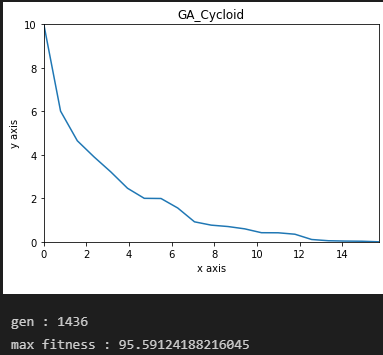
같은 조건으로 구간을 30개로 나눠 돌려본 모습이다.
너무 구간이 많아도 좋지는 않은 것 같다. 오히려 적합도가 떨어진다.
또한 정규화시 기울기가 계속 커지거나 작아지는 현상이 반복되어 이렇게 극단적으로 변하는것 같다.

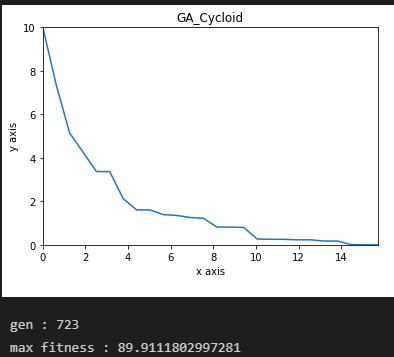
x_size = 25일때이다.

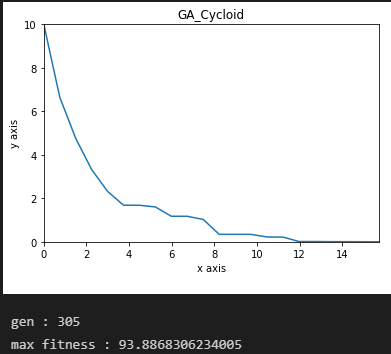
x_size = 21이다.

x_size = 19이다.

이쯤이면 어떻게 20일때가 그렇게 높게 나왔는지 의심이 가는 수준이다.

< 그저 독보적이다.. >

이렇게 된거 구간의 길이 뿐만이 아니라 다른 것들도 건드려 보자.

http://www.aistudy.com/biology/genetic/operator_moon.htm#_bookmark_1a19850

유전 알고리즘의 연산자들 : 문병로

또한, 이 책에서는 '룰렛 휠 방식'을 사용해 다음 세대로 이동될 유전자를 선택하는데, 이 과정에서 특이한 적합도 함수를 사용한다.

초보자들이 유전 알고리즘을 처음 구현하면서 흔히 범하는 실수는 위와 같이 k 를 사용해서 적합도를 조정하지 않고 주어진 문제에서의 해의 품질을 그대로 적합도로 사용하는 것이다. 이렇게 하면 대부분의 경우 해 집단에서 가장 좋은 해와 가장 나쁜 해의 품질이 너무 차이가 나서, 적합도에 비례해서 선택 기회를 갖게 되면 나쁜 해 들은 거의 선택될 기회를 잃게 된다. 결과적으로 엄청나게 큰 선택압을 주어 해의 다양성을 급속히 떨어뜨리는 결과를 부르게 된다.

필자는 현재 (T/t)^2을 적합도 함수로 사용하는데(T : 최소 시간, t : 실제 걸린 시간), 해당 방법은 적합도 차이를 '매우 크게' 부각하는 방법이라 개선이 필요할 것 같았다.

그런데 해당 함수가 이해가 되지 않아 다른 식을 생각해 보기로 하였다.

고민을 해 보다, 지수 함수 형태의 식이 적당하다 판단하였고, 마침 필자의 친구가 시그모이드 함수를 얘기해 주어 해당 함수를 적용해보려 하였다.

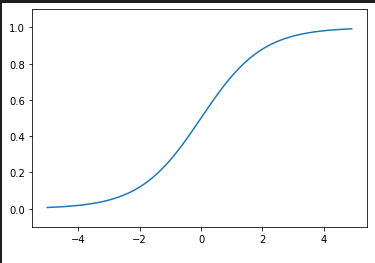
처음엔 꽤 잘 나오는 것 같았다.
그래서 범위를 늘려 보자

< Sigmoid in Python >

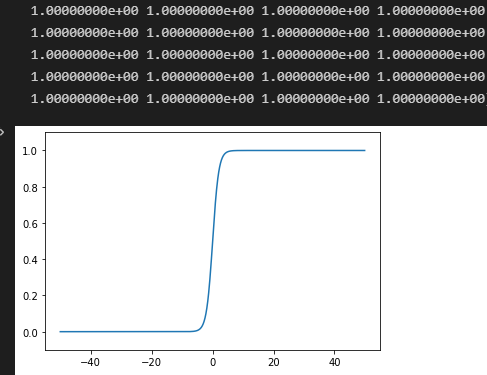
실수부를 처리하지 못해 수렴하는 모습을 보인다.
표기되는 소수 자리를 늘리는 방법을 찾을 수도 있겠지만, 시간이 없어 다음에 하도록 하자.